Drill & Ceremonies - Column Right (Left)
|
|
Column Movements:
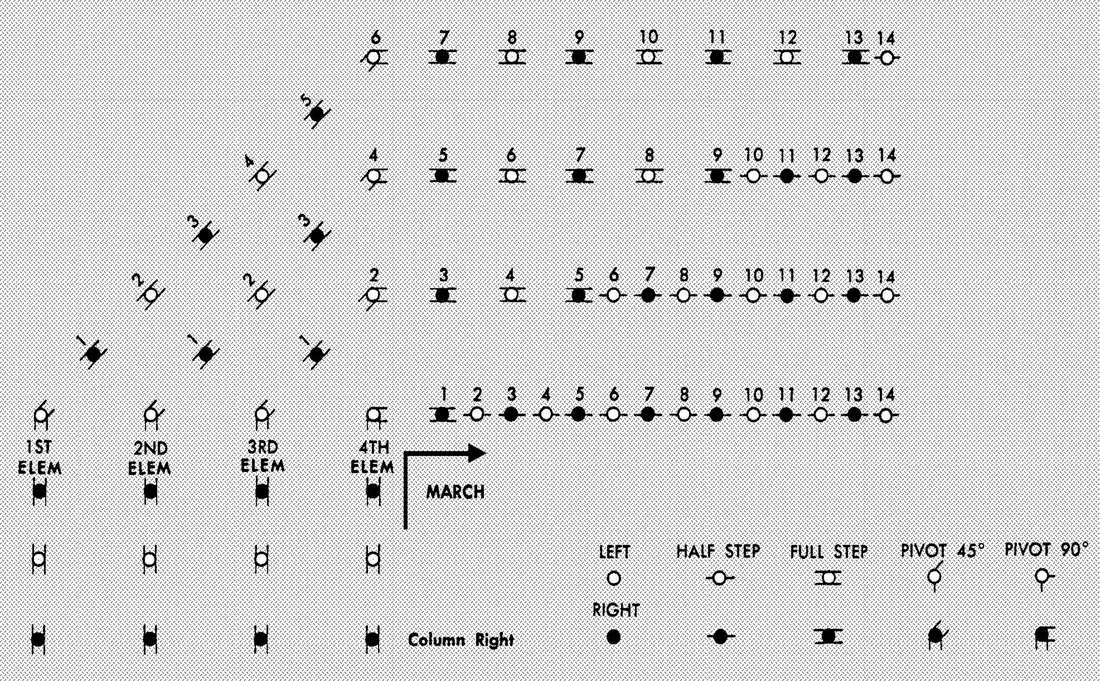
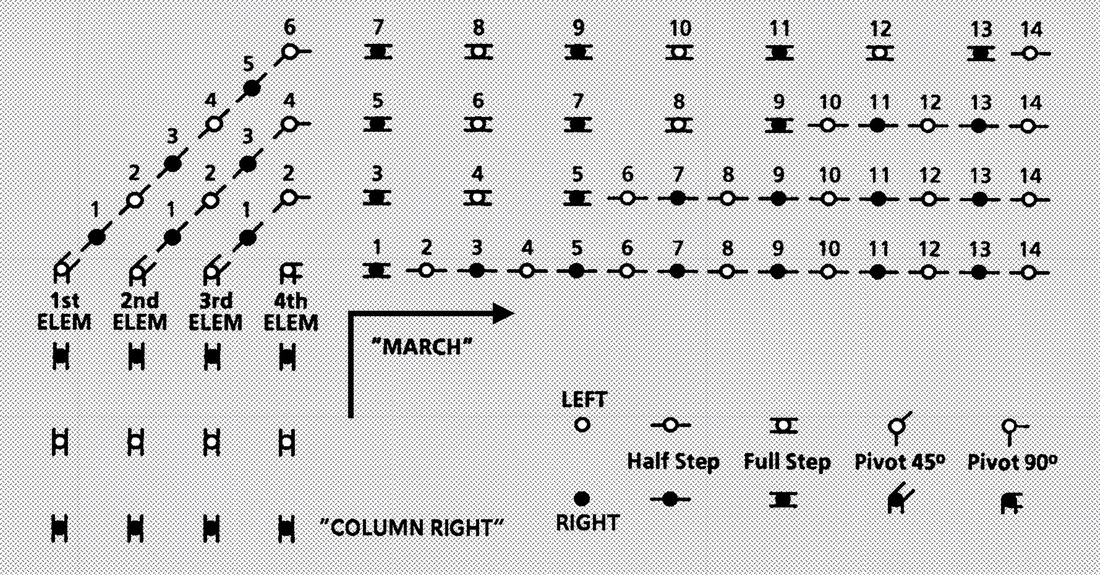
1. Column Right (Left) Normal Interval (Marching). The commands are Column Right (Left), MARCH and Forward, MARCH (Figure 4.6 and Figure 4.7). 1.1. On the command Column Right (Left), MARCH, the fourth (first) element leader takes one more 24-inch step, pivots 90 degrees to the right (left) on the ball of the left (right) foot, and suspends armswing during the pivot. Following the pivot, step off in a 24-inch step and resume coordinated armswing. Beginning with the second step after the pivot, take up the half step. Each succeeding member of the fourth (first) element marches to the approximate pivot point established by the person in front of him or her and performs the same procedures as the element leader. 1.2. The third (second) element leader takes one 24-inch step, (maintaining coordinated arm swing throughout) pivots 45 degrees to the right (left) on the ball of the left (right) foot, and takes two 24-inch steps prior to pivoting 45 degrees to the right (left) on the ball of the left (right) foot. Continue marching in 24-inch steps until even with the person who marches on the right (left). Then begin half stepping and establish interval and dress. Each succeeding member of the third (second) element marches to the approximate pivot point established by the person in front of him or her and performs the same procedures as the element leader. 1.3. The second (third) element leader takes one more 24-inch step, (maintaining coordinated armswing throughout) pivots 45 degrees to the right (left) on the ball of the left (right) foot, and takes four 24-inch steps prior to pivoting 45 degrees to the right (left) on the ball of the left (right) foot. Continue marching in 24-inch steps until even with the person who marches on the right (left). Then begin half stepping, and establish interval and dress. Each succeeding member of the second (third) element marches to the approximate pivot point established by the person in front of him or her and performs the same procedures as the element leader. 1.4. The first (fourth) element leader takes one more 24-inch step, (maintaining coordinated armswing throughout) pivots 45 degrees to the right (left) on the ball of the left (right) foot, and takes six 24-inch steps prior to pivoting 45 degrees to the right (left) on the ball of the left (right) foot. Continue marching in 24-inch steps until even with the person who marches on the right (left). Then begin half stepping, and establish interval and dress. Each succeeding member of the first (fourth) element marches to the approximate point established by the person in front of him or her and performs the same procedures as the element leader. 1.5. The guide performs the pivots and steps exactly as the fourth element leader. Following completion of the pivots, the guide continues in a 24-inch step until he or she is ahead of the fourth element leader. The guide pivots 45 degrees to a position in front of the fourth element leader; then he or she pivots 45 degrees again toward the front and begins half stepping. 1.6. Once the entire formation has changed direction and dress, cover, interval, and distance are reestablished, Forward, MARCH will be given. On the command MARCH, take one more 12-inch step with the right foot, then step off with a full 24-inch step with the left foot. When performing column left, the responsibility of dress reverts to the left flank on the preparatory command Column left. The responsibility remains with the left flank until the command MARCH is given; then it reverts to the right flank. 2. Column Right (Left) Close Interval. These movements are performed in the same manner as at normal interval except the element closest to the base file takes two 12-inch steps between pivots, the next element takes four 12-inch steps between pivots, and the last element takes six 12-inch steps between pivots. 3. Column Movements from a Halt (Normal or Close Interval). When column movements are executed from a halt, procedures are similar to those in paragraph 1. On the command MARCH, element leaders begin the movement by executing a face in marching for a column left. For a column right, element leaders take one 24-inch step forward, then execute the movement. 4. Column Half Right (Left): 4.1. To change the direction of a column by 45 degrees, the command is Column Half Right (Left), MARCH. On the command MARCH, the leading cadet of the right (left) flank advances one full 24inch step, pivots 45 degrees to the right (left) on the ball of the left (right) foot, and advances another full 24-inch step, maintaining coordinated armswing. The cadet then takes up the half step and continues in a half step until each member in his or her rank is abreast of each other. Then all members of that rank resume a full 24-inch step. In the meantime, the remaining individuals of the leading rank pivot 45 degrees to the right (left), with coordinated armswing and without changing the interval, and continue marching in full 24-inch steps until they are abreast of the base file. At this point, they conform to the step of the individual in the right (left) flank and establish the proper interval. The remaining airmen in each file march to the approximate pivot point established by the element leader and perform the movement in the same manner. They then dress to their right and cover directly behind the person in front of them. 4.2. The flight commander and guide pivot 45 degrees in the direction of the movement. Then they pivot 45 degrees back to their original positions in front of the column. 4.3. When column half right (left) is executed from a halt, the procedures are the same as described in paragraph 4.1 above except, on the command of execution, the element leaders begin the movement by executing a face in marching to the indicated direction. 4.4. To execute a slight change of direction, the command INCLINE TO THE RIGHT (LEFT) is given. The guide or guiding element moves in the indicated direction, and the rest of the element follows. There is no pivot in this movement. |